Time Aware Symbols#

The TimeAwareSymbol object is an extension of sympy.Symbol. It is an important building block of DSGE models. This short tutorial shows what they are, and how they can be used.

import sys

sys.path.append("/Users/jessegrabowski/Documents/Python/gEconpy/")

import sympy as sp

from gEconpy.classes.time_aware_symbol import TimeAwareSymbol

Basic Functionality#

A TimeAwareSymbol functions exactly like sp.Symbol, except that it accepts a time_index argument. time_index is an integer that gives an offset from time t. Here are three examples:

x_t = TimeAwareSymbol("x", time_index=0)
x_tm1 = TimeAwareSymbol("x", time_index=-1)
x_tp1 = TimeAwareSymbol("x", time_index=1)

x_t
\[\displaystyle x_{t}\]
x_tm1
\[\displaystyle x_{t-1}\]
x_tp1
\[\displaystyle x_{t+1}\]

The variable is build from the provided base_name (in this case x), and the time_index. The name is constructed by combining these two elements.

x_t.name

'x_t'

x_t.base_name

'x'

x_t.time_index

0

There is also a safe_name, which can be used in contexts where the + or - in the name would be problematic. For the safe_name, + is replaced with p, and - with m.

x_tp1.name

'x_t+1'

x_tp1.safe_name

'x_tp1'

x_tm1.safe_name

'x_tm1'

Otherwise, all other arguments to sp.Symbol can be specified. For example, assumptions are allowed:

x_t_positive = TimeAwareSymbol("x", time_index=0, positive=True)
x_t_positive
\[\displaystyle x_{t}\]
x_t_positive.assumptions0

{'positive': True,
 'finite': True,
 'negative': False,
 'commutative': True,
 'complex': True,
 'extended_positive': True,
 'imaginary': False,
 'extended_nonzero': True,
 'zero': False,
 'extended_nonpositive': False,
 'extended_real': True,
 'hermitian': True,
 'nonnegative': True,
 'nonzero': True,
 'nonpositive': False,
 'real': True,
 'extended_negative': False,
 'infinite': False,
 'extended_nonnegative': True}

Time manipulations#

After creation, several methods for manipulating the time index of the variable are available:

  • step_forward increments the time_index

  • step_backward decremetes the time_index

  • set_t allows time_index to be set directly

x_t.step_forward()
\[\displaystyle x_{t+1}\]
x_t.step_backward()
\[\displaystyle x_{t-1}\]

The most important feature of TimeAwareSymbols is that when two TimeAwareSymbols have the same base_name and time_index, they evaulate as equal

x_t.step_backward() == x_tm1

True

x_t.step_forward() == x_tp1

True

Steady State#

Another important concept in analysis of dynamic systems is a “steady state”. A steady state is an equlibrium such that \(x_t = x_{t+1} = x_{t+1} = \dots = x_{ss}\)

Variables can be sent to the steady state using the to_ss method

x_t.to_ss()
\[\displaystyle x_{ss}\]

Since ‘ss’ is a special time_index, variables of the same base_name sent to the steady state will evaluate to equal

x_t.to_ss() == x_tp1.to_ss()

True

Working with Equations#

TimeAwareSymbols subclass Symbol, so anything you can do with a symbol can be done with a TimeAwareSymbol.

For example, you can do algebraic manipulations

eq = sp.Eq(x_tp1, (x_t + x_tm1) / 2)
eq
\[\displaystyle x_{t+1} = \frac{x_{t}}{2} + \frac{x_{t-1}}{2}\]

Or call sympy.solve

sp.solve(eq, x_t)[0]
\[\displaystyle 2 x_{t+1} - x_{t-1}\]

Usually, though, you are going to want to manipulate the time indices for entire expressions. Unfortunately, there is no TimeAwareExpr. Instead, gEconpy gives some helper functions for manipulation of equations that include TimeAwareSymbols. These are:

  • step_equation_forward

  • step_equation_backward

  • eq_to_ss

The equations do what the names suggest

from gEconpy.utilities import (
    eq_to_ss,
    step_equation_backward,
    step_equation_forward,
)

step_equation_forward(eq)
\[\displaystyle x_{t+2} = \frac{x_{t}}{2} + \frac{x_{t+1}}{2}\]
step_equation_backward(eq)
\[\displaystyle x_{t} = \frac{x_{t-1}}{2} + \frac{x_{t-2}}{2}\]
eq_to_ss(eq.lhs - eq.rhs)
\[\displaystyle 0\]

Example 1: \(AR(1)\) to \(MA(\infty)\)#

Using these tools, we can do powerful analysis on time series.

Consider an AR(1) system:

\[ x_t = \rho x_{t-1} + \epsilon_t\]

We can use step_equation_backward together with repeated substitution to derive the \(MA(\infty)\) form of the \(AR(1)\) system

eps_t = TimeAwareSymbol("\\varepsilon", 0)
rho = sp.Symbol("rho", positive=True)

# This is only the right-hand side, remember there's an x_t on the left
ar_1_rhs = rho * x_tm1 + eps_t

We will iterative shift the equation backwards and substitute

curr_x = x_t
curr_rhs = ar_1_rhs.copy()
for _ in range(10):
    display(sp.Eq(x_t, ar_1_rhs))
    curr_x = curr_x.step_backward()
    curr_rhs = step_equation_backward(curr_rhs)
    ar_1_rhs = ar_1_rhs.subs({curr_x: curr_rhs}).expand()
\[\displaystyle x_{t} = \rho x_{t-1} + \varepsilon_{t}\]
\[\displaystyle x_{t} = \rho^{2} x_{t-2} + \rho \varepsilon_{t-1} + \varepsilon_{t}\]
\[\displaystyle x_{t} = \rho^{3} x_{t-3} + \rho^{2} \varepsilon_{t-2} + \rho \varepsilon_{t-1} + \varepsilon_{t}\]
\[\displaystyle x_{t} = \rho^{4} x_{t-4} + \rho^{3} \varepsilon_{t-3} + \rho^{2} \varepsilon_{t-2} + \rho \varepsilon_{t-1} + \varepsilon_{t}\]
\[\displaystyle x_{t} = \rho^{5} x_{t-5} + \rho^{4} \varepsilon_{t-4} + \rho^{3} \varepsilon_{t-3} + \rho^{2} \varepsilon_{t-2} + \rho \varepsilon_{t-1} + \varepsilon_{t}\]
\[\displaystyle x_{t} = \rho^{6} x_{t-6} + \rho^{5} \varepsilon_{t-5} + \rho^{4} \varepsilon_{t-4} + \rho^{3} \varepsilon_{t-3} + \rho^{2} \varepsilon_{t-2} + \rho \varepsilon_{t-1} + \varepsilon_{t}\]
\[\displaystyle x_{t} = \rho^{7} x_{t-7} + \rho^{6} \varepsilon_{t-6} + \rho^{5} \varepsilon_{t-5} + \rho^{4} \varepsilon_{t-4} + \rho^{3} \varepsilon_{t-3} + \rho^{2} \varepsilon_{t-2} + \rho \varepsilon_{t-1} + \varepsilon_{t}\]
\[\displaystyle x_{t} = \rho^{8} x_{t-8} + \rho^{7} \varepsilon_{t-7} + \rho^{6} \varepsilon_{t-6} + \rho^{5} \varepsilon_{t-5} + \rho^{4} \varepsilon_{t-4} + \rho^{3} \varepsilon_{t-3} + \rho^{2} \varepsilon_{t-2} + \rho \varepsilon_{t-1} + \varepsilon_{t}\]
\[\displaystyle x_{t} = \rho^{9} x_{t-9} + \rho^{8} \varepsilon_{t-8} + \rho^{7} \varepsilon_{t-7} + \rho^{6} \varepsilon_{t-6} + \rho^{5} \varepsilon_{t-5} + \rho^{4} \varepsilon_{t-4} + \rho^{3} \varepsilon_{t-3} + \rho^{2} \varepsilon_{t-2} + \rho \varepsilon_{t-1} + \varepsilon_{t}\]
\[\displaystyle x_{t} = \rho^{10} x_{t-10} + \rho^{9} \varepsilon_{t-9} + \rho^{8} \varepsilon_{t-8} + \rho^{7} \varepsilon_{t-7} + \rho^{6} \varepsilon_{t-6} + \rho^{5} \varepsilon_{t-5} + \rho^{4} \varepsilon_{t-4} + \rho^{3} \varepsilon_{t-3} + \rho^{2} \varepsilon_{t-2} + \rho \varepsilon_{t-1} + \varepsilon_{t}\]

Since \(\rho \in (0, 1)\), the leading term will eventually go to zero, and we recover the well-known equation:

\[ x_t = \sum_{s=0}^t \rho^s \varepsilon_{t-s}\]

I don’t know any way for sympy to automatically detect the presence of this series and rewrite into summation notation – if you do, open an issue so I can update this example!

Example 2: Analytical Steady State#

More useful, perhaps, is that we can use TimeAwareSymbols to derive the steady state of a dynamical system. Consider the AR(1) equation again:

ar_1 = sp.Eq(x_t, rho * x_tm1 + eps_t)
ar_1
\[\displaystyle x_{t} = \rho x_{t-1} + \varepsilon_{t}\]

We can send this to the steady-state and compute the value of \(x_{ss}\)

sp.solve(eq_to_ss(ar_1), x_t.to_ss())[0]
\[\displaystyle - \frac{\varepsilon_{ss}}{\rho - 1}\]

Obviously we need to know something about \(\varepsilon_{ss}\). We typtically assume \(\varepsilon_t ~ N(0, \sigma)\). In the (deterministic!) steady state, there are no shocks, so \(\varepsilon_{ss} = 0\).

Let’s generalize the equation to allow a drift in the shocks, so \(\varepsilon_t ~ N(\mu, \sigma)\). We can pull out the \(\mu\) using the properties of normal distributions to obtain:

\[x_t = \mu + \rho x_{t-1} + \varepsilon_t\]
mu = sp.Symbol("mu")
ar_1 = sp.Eq(x_t, mu + rho * x_tm1 + eps_t)
ar_1
\[\displaystyle x_{t} = \mu + \rho x_{t-1} + \varepsilon_{t}\]

Solving for the steady state gives the well-known expression for the AR(1) steady state

sp.solve(eq_to_ss(ar_1).subs({eps_t.to_ss(): 0}), x_t.to_ss())[0]
\[\displaystyle - \frac{\mu}{\rho - 1}\]

Example 3: Deterministic RBC#

Consider an RBC model defined (in reduced form) as follows:

C, K, A, epsilon = [TimeAwareSymbol(x, 0) for x in ["C", "K", "A", "\\varepsilon"]]
alpha, beta, delta, rho = sp.symbols(
    "alpha beta delta rho",
)

euler = C.step_forward() / C - beta * (alpha * sp.exp(A.step_forward()) * K.step_forward() ** (alpha - 1) + 1 - delta)
transition = K.step_forward() - (sp.exp(A) * K**alpha + (1 - delta) * K - C)
shock = A - rho * A.step_backward() - epsilon

system = [euler, transition, shock]
for eq in system:
    display(eq)
\[\displaystyle - \beta \left(\alpha K_{t+1}^{\alpha - 1} e^{A_{t+1}} - \delta + 1\right) + \frac{C_{t+1}}{C_{t}}\]
\[\displaystyle C_{t} - K_{t} \left(1 - \delta\right) - K_{t}^{\alpha} e^{A_{t}} + K_{t+1}\]
\[\displaystyle - \rho A_{t-1} + A_{t} - \varepsilon_{t}\]

We can use TimeAwareSymbols to solve for the deterministic steady state of this entire system in one fell swoop

ss_system = [eq_to_ss(eq).simplify().subs({epsilon.to_ss(): 0.0}) for eq in system]
ss_dict = sp.solve(ss_system, [K.to_ss(), C.to_ss(), A.to_ss()], dict=True)[0]

for var, eq in ss_dict.items():
    display(sp.Eq(var, eq))
\[\displaystyle A_{ss} = 0\]
\[\displaystyle C_{ss} = - \delta \left(\frac{\beta \left(\delta - 1\right) + 1}{\alpha \beta}\right)^{\frac{1}{\alpha - 1}} + \left(\left(\frac{\beta \left(\delta - 1\right) + 1}{\alpha \beta}\right)^{\frac{1}{\alpha - 1}}\right)^{\alpha}\]
\[\displaystyle K_{ss} = \left(\frac{\beta \delta - \beta + 1}{\alpha \beta}\right)^{\frac{1}{\alpha - 1}}\]

Using sp.lambdify, we can compile a function that computes the steady state of the system given input parameters. This is essentially what gEconpy does internally when solving for the steady state of a DSGE model.

f_ss = sp.lambdify([alpha, beta, delta, rho], list(ss_dict.values()))
param_dict = {"alpha": 0.33, "beta": 0.99, "delta": 0.035, "rho": 0.95}
f_ss(**param_dict)

[0, 1.9825902234443513, 19.50030034168597]

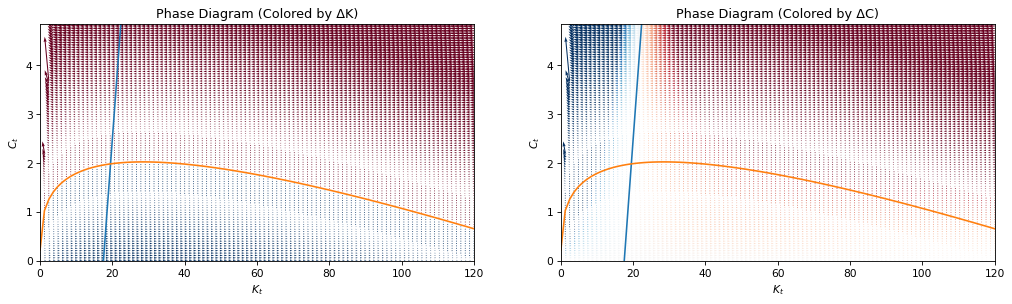
Phase Diagram#

Since this system is deterministic, we can construct a phase diagram showing system dynamics for a given \((C_t, K_t)\) tuple. To do this, we first need to re-arrange the Euler equation and law of motion of capital to obtain rates of change, \(\Delta C_{t+1}\) and \(\Delta K_{t+1}\). For \(\Delta C_{t+1}\) we get:

\[\begin{split}\begin{align} \Delta C_{t+1} &= C_{t+1} - C_t \\ &= \beta C_t \left (\alpha K_{t+1}^{\alpha - 1} + (1 - \delta) \right ) - C_t \\ &= \left (\beta \alpha K_{t+1}^{\alpha - 1} + \beta (1 - \delta) - 1 \right ) C_t \end{align}\end{split}\]

For the second line, the Euler equation was solved for \(C_{t+1}\) and substituted.

For \(\Delta K_{t+1}\):

\[\begin{split}\begin{align} \Delta K_{t+1} &= K_{t+1} - K_t \\ &= K_t^\alpha + (1 - \delta) K_t - C_t \\ \end{align}\end{split}\]

Computing these \(\Delta\)s over a grid of points will give us a phase diagram. Let’s look at how these can be solved for with sympy:

C_tp1 = sp.solve(euler, C.set_t(1))[0]
C_tp1
\[\displaystyle \beta C_{t} \left(\alpha K_{t+1}^{\alpha - 1} e^{A_{t+1}} - \delta + 1\right)\]
Delta_C = (C_tp1 - C).collect(C).subs({A.set_t(1): 0})
Delta_C
\[\displaystyle C_{t} \left(\beta \left(\alpha K_{t+1}^{\alpha - 1} - \delta + 1\right) - 1\right)\]

This solution isn’t exactly what we need, though, because we don’t want the \(K_{t+1}\). Use the transition equation to write it in terms of time \(t\) variables only

K_tp1 = sp.solve(transition.subs({A: 0}), K.set_t(1))[0]
Delta_C = Delta_C.subs({K.set_t(1): K_tp1})
Delta_C
\[\displaystyle C_{t} \left(\beta \left(\alpha \left(- \delta K_{t} - C_{t} + K_{t} + K_{t}^{\alpha}\right)^{\alpha - 1} - \delta + 1\right) - 1\right)\]
K_tp1 = sp.solve(transition, K.set_t(1))[0].subs({A: 0})
K_tp1
\[\displaystyle - \delta K_{t} - C_{t} + K_{t} + K_{t}^{\alpha}\]
Delta_K = K_tp1 - K
Delta_K
\[\displaystyle - \delta K_{t} - C_{t} + K_{t}^{\alpha}\]

Compile a function with sp.lambdify

parameters = list(param_dict.keys())
f_Delta = sp.lambdify([C, K, *parameters], [Delta_C, Delta_K])

We are also interested in when \(\Delta C_{t+1} = \Delta K_{t+1} = 0\), because these equations will form boundaries in phase space. We can do this by using sp.solve.

First, solve \(\Delta C_{t+1}\) for \(C_t\). There will be two solutions, and one will be zero (since the whole expression is multiplied by \(C_t\)). We’re only interested in the non-trivial solution.

boundary_1 = sp.solve(Delta_C, C)[1]
boundary_1
\[\displaystyle - \delta K_{t} + K_{t} + K_{t}^{\alpha} - \left(\frac{\beta \delta - \beta + 1}{\alpha \beta}\right)^{\frac{1}{\alpha - 1}}\]

Next, solve \(\Delta K_{t+1}\) for \(C_t\)

boundary_2 = sp.solve(Delta_K, C)[0]
boundary_2
\[\displaystyle - \delta K_{t} + K_{t}^{\alpha}\]

Compile a function

f_boundaries = sp.lambdify([K, *parameters], [boundary_1, boundary_2])

Functions created with sp.lambdify are inherently vectorized, so we can make a grid of capital values and compute the associated consumpions

import matplotlib.pyplot as plt
import numpy as np

k_max = 120
c_max = k_max ** param_dict["alpha"]  # We can't consume more than exists in the economy!

k_grid = np.linspace(1e-2, k_max, 100)
c_grid = np.linspace(1e-2, c_max, 100)
boundaries = f_boundaries(k_grid, **param_dict)

kk, cc = np.meshgrid(k_grid, c_grid)
with np.errstate(divide="ignore", invalid="ignore"):
    c_delta, k_delta = f_Delta(cc, kk, **param_dict)

fig, ax = plt.subplots(1, 2, figsize=(16, 4), dpi=77)
for axis, colorby, name in zip(fig.axes, [k_delta, c_delta], ["ΔK", "ΔC"], strict=False):
    axis.plot(k_grid, boundaries[0], label="ΔK = 0")
    axis.plot(k_grid, boundaries[1], label="ΔC = 0")
    quiver_plot = axis.quiver(kk, cc, k_delta, c_delta, colorby, cmap=plt.cm.RdBu, clim=(-0.05, 0.05))
    axis.set(
        xlim=(0, k_max),
        ylim=(0, c_max),
        xlabel="$K_t$",
        ylabel="$C_t$",
        title=f"Phase Diagram (Colored by {name})",
    )
plt.show()
../../_images/14a5428f32e2172a5e544397babf04d2f3e3335f82bf451ecb10884cc9f82daf.png

Authors#

  • Authored by Jesse Grabowski in March 2025

Watermark#

%load_ext watermark
# Delete lambdify functions (they break watermark)
del f_ss, f_Delta, f_boundaries

%watermark -n -u -v -iv -w -p gEconpy

Last updated: Sat Mar 15 2025

Python implementation: CPython
Python version       : 3.12.9
IPython version      : 9.0.1

gEconpy: 0+untagged.305.gd931e48.dirty

sympy     : 1.12.1
sys       : 3.12.9 | packaged by conda-forge | (main, Feb 14 2025, 07:56:32) [Clang 18.1.8 ]
gEconpy   : 0+untagged.305.gd931e48.dirty
numpy     : 1.26.4
matplotlib: 3.10.1

Watermark: 2.5.0